Shihanmax's blog

< Back

XGBoost理解

XGBoost（eXtreme Gradient Boosting）是GBDT的一种高效的工程实现，在数据竞赛中应用十分广泛。

下文从决策树的定义开始，介绍决策树的分裂指标、决策树在boosting算法中的应用BDT、引入残差信息的Gradient boosting算法等，最后，介绍集成了多种高效算法的XGBoost的工程实现。

一、决策树

决策树是一种描述对实例进行分类的属性结构，由节点和有向边组成，其中，节点分为内部节点和叶子结点，内部节点表示特征或属性，叶子结点表示一个类。

从根节点开始，对样本的某一个特征进行测试，根据结果，将样本划分到其若干个子节点中，其中每个子节点均对应该特征的一个取值；针对每一个子节点，继续选取一个特征重复执行上述过程，直到将实例划分到叶节点所对应的类别当中。

在上述描述过程中，有一个重要的点是，如何选择一个最好的特征，并使用其进行样本的划分？

直观上考虑，如果划分后的子集拥有更高的“纯度”，则表示该特征是一个好的特征。所谓纯度是指，划分后的子样本集合所对应的类别应尽可能一致，极端考虑，假设我们选择了一个特征，在使用此特征进行划分后，所有的子集合中，样本的类别几乎一致，则可以认为这个特征是一个非常强的特征。

在决策树实现过程中，一般使用三个指标衡量分类纯度：信息增益、信息增益比、基尼指数。首先回顾一下信息论中几个基础的概念：

熵（Entropy）

设$X$是随机变量，$P(X=x_i)=p_i,i=1,2,…,n$，则$X$的熵定义为：

\[H(X)=-\sum_\limits{i=1}^{n}{p_i}\log{p_i}\]

可以看出，$X$的熵的取值仅与$X$的分布有关，与$X$的取值无关，所以这里$H(X)$也可以写作$H(p)$。上式中的对数以$2$为底时，熵的单位为$bit$；以$e$为底时对应的单位为$nat$。

熵可以用来衡量随机变量的不确定性。

条件熵

条件熵$H(Y\mid X)=\sum_\limits{i=1}^{n}{p_i}H(Y\mid X=x_i)$，其中，$p_i=P(X=x_i),i=1,2,…,n$。

条件熵$H(Y\mid X)$表示，在已知随机变量$X$时，随机变量$Y$的不确定性。

信息增益（互信息）

信息增益定义为：$MI(Y,X)=H(Y)-H(Y\mid X)$，表示“得知$X$的信息，而使$X$的不确定性减少的程度”。

在决策树的特征选择过程中，使用特征$A$对数据集$D$进行分割，所带来的信息增益可以表示为：$g(D,A)=MI(D,A)=H(D)-H(D\mid A)$

信息增益比

有以上定义可知，通过计算信息增益来进行数据分割时，会偏向取值较多的特征的问题，针对此问题，使用信息增益比来进行修正：

$g_{R}(D,A)=\frac{g(D,A)}{H_{A}(D)}$，其中$H_A(D)=-\sum_\limits{i=1}^{n}{\frac{\mid D_i\mid}{\mid D\mid}}\log{\frac{\mid D_i\mid}{\mid D\mid}}$，即计算数据集$D$的熵时，特征$A$的贡献。

基尼指数Gini Index

在分类问题中，假设有$k$个类别，样本属第$k$类的概率为$p_k$，则概率分布的基尼指数定义为：

\[Gini(p)=\sum_\limits{k=1}^{K}p_k(1-p_k)=1-\sum_\limits{k=1}^{K}p_k^2\]

则数据集$D$的基尼指数为：

\[Gini(D)=1-\sum_\limits{k=1}^{K}\frac{\mid C_k\mid}{\mid D \mid}\]

其中，$C_k$表示第$k$类样本子集的大小。

假设有特征A，根据特征$A$是否满足特定条件，将数据集划分为两部分：$D_1,D_2$，则可以定义：给定特征$A$的条件下，样本集合$D$的基尼指数$Gini(D,A)$（即给定特征$A$后，样本集合$D$的不确定性减少的程度）：

\[Gini(D,A)=\frac{\mid D_1\mid}{\mid D \mid}Gini(D_1)+\frac{\mid D_2\mid}{\mid D \mid}Gini(D_2)\]

在决策树的构建阶段，我们便可以在进行最优特征选择时，遍历所有的特征，然后计算出其纯度指标（信息增益、信息增益比、基尼指数），然后选出一个指标最高的特征，并根据该特征的取值将样本集合分裂。

常用的决策树算法有ID3算法、C4.5算法和CART算法，其中ID3算法使用信息增益进行特征选择；C4.5算法进行了改进，使用信息增益比进行特征选择；对于分类树，CART算法使用基尼指数最小化准则，对于回归树，使用平方误差最小化准则。

二、回归树

树模型在机器学习领域中的应用场景主要有两类：分类任务与回归任务，二者都是由特征到标签的影射，区别在于，分类树的标签是一个类别，而回归树的标签是一个连续的值。

上文提到，对于分类树，可以使用信息增益、信息增益比、基尼指数来进行树节点的分类决策，而回归树则无法使用这些指标。

CART（Classification and Regression Tree，分类与回归树）是分类树和回归树的统称。在回归任务中，CART假设树是二叉树，通过不断地对特征进行分裂（使用该特征对样本空间进行划分）生成一棵树。

我们可以把回归树认为是一个函数$f$，它能够将输入样本的特征映射为一个分数。在集成模型中，多棵CART树的预测结果的加和作为模型最终的预测结果。

回归树有两类参数：树的结构和叶子结点的分数。回归树的学习过程即是树的结构和叶子结点分数的学习。也即学习函数$f$。如何对函数进行学习呢？需要定义一个目标函数，然后优化该目标函数。

回归树不止可以做回归任务：分类、回归、排序等都可以使用，取决于如何定义目标函数。例如，当我们使用平方损失$l(y_i,\hat{y_i})=(y_i-\hat{y_i})^2$时，就变成了梯度提升机（Gradient boosted machine, GBM）；而使用Logistic loss$l(y_i,\hat{y_i})=y_i\ln(1+e^{-\hat{y_i}})+(1-y_i)\ln(1+e^{\hat{y_i}})$时，就变成了LogitBoost。

三、Boosting

Boosting是集成学习思想的一种（另一种集成学习思想是Bagging，指并列地训练多个基模型，并通过投票（分类问题）或平均（回归问题）的方式计算得到最终的集成结果）。

Boosting算法的执行流程是串行的，即后面的模型的训练依赖前面的模型的预测结果。典型的算法有Adaboost、GBDT等。下面简单介绍这两类算法。

3.1 Adaboost

Adaboost算法（Adaptive Boosting，自适应增强）是boosting算法的代表，其特点是通过迭代训练一系列基分类器，在每次迭代过程中，提高被前一个分类器分错的样本的权重，降低被前一个分类器分对的样本的权重。最后，Adaboost算法将基分类器进行加权线性组合，每个基分类器都有一个权重，分类误差越小的基分类器，其权重越高，否则权重越低。

Adaboost的执行流程简述如下：

首先，初始化数据集为等权重。接着，依次迭代训练$M$个基模型$G_1,G_2,…,G_M$，针对模型$G_m$，执行以下四步：

  1. 使用带权的数据训练$G_m$
  2. 计算$G_m$在数据集上的带权分类误差率
  3. 通过此误差率计算分类器的权重
  4. 通过带权基模型$G_m$的预测结果，更新训练数据的权重

在$M$个基模型训练完成后，每个基模型均有一个权重，使用该权重对一系列基模型进行加权组合，即可得到最终的分类器。

3.2 GBDT

GBDT全称是Gradient Boost Desision Tree，即梯度提升决策树。与Adaboost不同的是，GBDT的每次迭代目标是减小之前模型的残差，在残差减小的方向（负梯度方向）建立一个新的模型。

例如：

假设样本$[(1,2,3), 4]$，其中$(1,2,3)$是样本特征，$4$是样本标签

假设模型$m_i$在上述样本上的预测结果是$3.6$

则模型$m_{i+1}$的拟合目标就变为：$[(1,2,3), 0.4]$

按上述方式得到一系列基模型后，GBDT的预测值就是样本在所有基模型上的结果的加和。

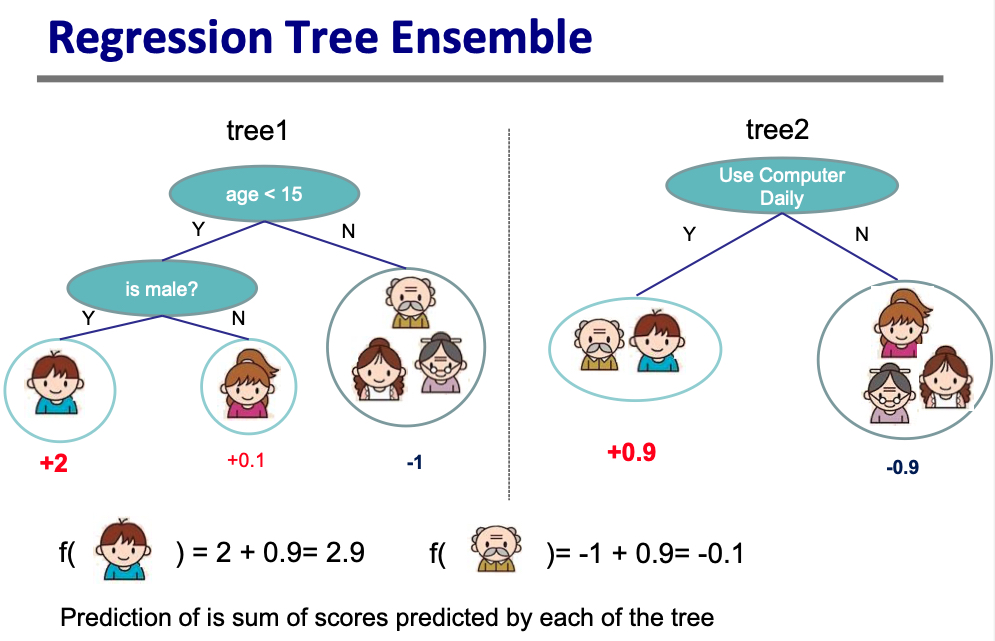
regression tree ensemble

图1 Regression Tree ensemble

在回归任务中，每一次迭代中对每一个样本都有一个预测值，损失函数使用MSE（均方误差损失）：$l(y_i,\hat{y_i})=\frac{1}{2}(y_i-\hat{y_i})^2$，对损失计算梯度取负：$-[\frac{\partial l(y_i,\hat{y_i})}{\partial \hat{y_i}}]=(y_i-\hat{y_i})$。

由上述结果可知，当损失函数使用MSE时，每一次拟合的值就是基模型的真实值减预测值，也即“残差”。

四、XGBoost

XGBoost是一个高效、灵活、可移植的分布式梯度提升工具包。是一种基于梯度提升框架的并行化的提升树实现方案。

XGBoost的思想是，不断地在训练过程中添加树，利用特征分裂来生长一棵树，添加树的过程就是拟合一个新函数的过程，这个新函数的拟合对象是上一次预测结果的残差。

\[\hat{y}=\phi(x_i)=\sum_\limits{k=1}^Kf_k(x_i)\]

训练完成后得到$K$棵树，针对一个样本，该样本的特征在$K$棵树上会落到$K$个叶子结点上，得到$K$个预测分数，将这些分数相加，就能得到该样本的预测值。

4.1 XGBoost的目标函数和误差

将XGBoost的误差可以简写如下：

\[L(\phi)=\sum_\limits{i}l(\hat{y_i}-y_i)+\sum_\limits{t}\Omega(f_t)\]

损失函数分为两部分，第一部分为误差函数，误差函数反映了当前模型对训练数据的拟合程度，其中$y_i$表示第$i$个样本的真实值，$\hat{y_i}$是所有基模型的输出累加；第二部分为正则化项，正则化项定义了模型的复杂度。

4.1.1 误差函数

观察目标函数的形式和模型的结构可知，我们不能使用像SGD一类的算法来寻找$f$，因为$f$不是一个数值向量而是一个函数，那么我们的目标其实是一个泛函。针对这种目标函数，解决方案是使用加法模型来训练。即从预测一个常数开始，每次（迭代轮次）增加一个新的函数，模型的预测结果为函数的预测结果加上一次预测的结果。

addition training

图2 加法模型的训练目标

训练过程中，第$t$轮的模型预测值$\hat{y}^{(t)}=\hat{y}^{(t-1)}+\epsilon f_t(x_i)$，其中$\epsilon$为缩减因子（shrinkage），是为了防止过拟合而设置的，一般取$0.1$（为简单起见，以下推导略去$\epsilon$）。

误差函数可以记为：$l(y_i,\hat{y}^{(t-1)},f_t(x_i))$，第$t$轮训练的目标是学习函数$f_t$，至此，XGBoost的目标函数$Obj^{(t)}$可以写为：

\[Obj^{(t)}=\sum\limits_{i=1}^n(l(y_i,\hat{y}^{(t-1)},f_t(x_i)) + \Omega(f_t)) +constant\]

在第$t$轮，我们的目标是寻找函数$f_t$，使得$Obj^{(t)}$最小化。

上面提到，当损失函数$l(\cdot)$为MSE时，我们可以推导出，损失函数的负梯度方向即是残差，那么，当损失函数是其他形式的函数呢？

XGBoost提出，对于其他形式的损失函数，则使用一个二次函数来近似，这里使用泰勒展开的方式。

回顾泰勒定理：

设有在$a$点所在区间上$n+1$阶可导的函数$f(x)$，则对这个区间上的任意$x$，都有如下泰勒展开形式：

\[f(x)=f(a)+\frac{f'(a)}{1!}(x-a) + \frac{f^{(2)}(a)}{2!}(x-a)^2+\cdot \cdot \cdot + \frac{f^{(n)}(a)}{n!}(x-a)^n + R_n(x)\]

其中，$R_n(x)$为余项，是$(x-a)^n$的高阶无穷小。

在XGBoost中，对损失函数进行了二阶泰勒展开：

\[f(x+\Delta x) \simeq f(x)+f^{\prime}(x) \Delta x+\frac{1}{2} f^{\prime \prime}(x) \Delta x^{2}\]

定义$g_{i}=\partial_{\hat{y}^{(t-1)}} l\left(y_{i}, \hat{y}^{(t-1)}\right), \quad h_{i}=\partial_{\hat{y}^{(t-1)}}^{2}l\left(y_{i}, \hat{y}^{(t-1)}\right)$

将$l(y_i,\hat{y}^{(t-1)}+f_t(x_i))$中的$\hat{y_i}^{(t-1)}$看作二阶泰勒展开式中的$x$；将$f_t(x_i)$看作展开式中的$\Delta x$，则目标函数可以近似写为：

\[Obj^{(t)} \simeq \sum_{i=1}^{n}\left[l\left(y_{i}, \hat{y}_{i}^{(t-1)}\right)+g_{i} f_{t}\left(x_{i}\right)+\frac{1}{2} h_{i} f_{t}^{2}\left(x_{i}\right)\right]+\Omega\left(f_{t}\right)+\text { constant }\]

在上式中，$l\left(y_{i}, \hat{y}_{i}^{(t-1)}\right)$为样本的真实标签和第$t-1$次预测的残差，是一个已知的数值，不影响第$t$轮的优化，常数项也可以移除，因此，目标函数可以重写为：

\[Obj^{(t)}=\sum_\limits{i=1}^{n}[g_{i} f_{t(x_{i})}+\frac{1}{2} h_{i} f_{t}^{2}(x_{i})]+\Omega (f_{t})\]

其中，$g_{i}=\partial_{\hat{y}^{(t-1)}} l\left(y_{i}, \hat{y}^{(t-1)}\right), \quad h_{i}=\partial_{\hat{y}^{(t-1)}}^{2}l\left(y_{i}, \hat{y}^{(t-1)}\right)$。

可以看出，目标函数仅依赖每个样本在误差函数上的一阶导数$g$和二阶导数$h$，这里也提示了XGBoost与GBDT在目标函数的一个差别：XGBoost考虑了误差函数的二阶导数。

4.1.2 正则化项

在树模型中，正则化项的加入一般是为了控制树的规模。XGBoost目标函数的正则化项的定义如下：

\[\Omega(f)=\gamma T+\frac{1}{2} \lambda\Vert w\Vert^2\]

其中，$T$表示叶子结点的个数，$w$表示叶子结点的分数，将二者作为惩罚项时，即要求在训练过程中，生成的树的叶子结点尽可能少，且叶子结点的数值不会过大，从而达到防止过拟合的目的。

4.1.3 XGBoost的目标函数

回顾上面得到的目标函数的表达式：

\[Obj^{(t)}=\sum_\limits{i=1}^{n}[g_{i} f_{t(x_{i})}+\frac{1}{2} h_{i} f_{t}^{2}(x_{i})]+\Omega (f_{t})\]

其中$f_t(x)$可以写为：

\[f_t(x)=w_{q(x)},\quad w\in\mathrm{R}^T,q:\mathrm{R}^d \rightarrow\{1,2,...,T\}\]

$w$表示树的叶子结点的权重，$q$表示树的结构，给定一个输入，结构函数将其映射到叶子结点的索引，再通过权重向量$w$（可以看到权重向量的维度为叶子结点的个数），得到对应的叶子结点的分数。

由以上定义，可以将上述目标函数修改为：

\[\begin{aligned} Obj^{(t)} & \simeq \sum_\limits{i=1}^n[g_i f_t(x_i)+\frac{1}{2}h_i f_t^2(x_i)] + \Omega(f_t) \\ &=\sum_{j=1}^{T}\left[\left(\sum_{i \in I_{j}} g_{i}\right) w_{j}+\frac{1}{2}\left(\sum_{i \in I_{j}} h_{i}+\lambda\right) w_{j}^{2}\right]+\gamma T \end{aligned}\]

其中$I_j$定义为叶子节点$j$上样本索引的集合：$I_{j}={i \mid q(x_{i})=j}$，值得注意的是，这一步的目标函数的转换有两种累加形式，第一个是样本角度的累加，通过引入$f_t(x)=w_{q(x)}$后，转化为叶子结点个数的累加。（回忆前述定义的树结构映射$q$，其能够将样本$x_i$映射到树的一个叶子结点上。）

至此，我们将目标函数转化为$T$个独立的二次函数。

在上述目标函数上，定义$G_j=\sum_\limits{i \in I_{j}} g_{i}$，$H_j=\sum_\limits{i \in I_{j}} h_{i}$，将目标函数简写为：

\[Obj^{(t)}=\sum_\limits{j=1}^T[G_jw_j+\frac{1}{2}(H_j+\lambda)w_j^2]+\gamma T\]

这是一个二次函数的最优化问题，假设此时树的结构已经确定，要计算$w_j$，可以将目标函数对$w_j$求偏导后另为$0$，可得：

\[w_j^*=-\frac{G_j}{H_j+\lambda}\]

上式衡量了树结构好的程度。将最优$w_j$代回目标函数表达式，有：

\[Obj=-\frac{1}{2} \sum_\limits{j=1}^{T} \frac{G_{j}^{2}}{H_{j}+\lambda}+\gamma T\]

4.2 XGBoost节点分裂

前面我们定义了XGBoost的目标函数$Obj$，它描述了在给定树结构的情况下，目标函数所能减少的最大幅度。我们可以将其称为“结构分数（structure score）”，基于此，接下来讨论一下XGBoost在建树过程中的一些细节。

4.2.1 XGBoost节点分裂方式

在树模型中，一棵树是由节点一分为二、生成的子节点继续分裂后逐渐形成的。那么XGBoost中节点的分裂方式有哪些呢？

1）贪心地枚举所有树的结构

由于上文可知，在确定了一个树的结构后，我们便可以计算出该结构下最好的分数。那么一个直观的想法是，枚举不同的树结构，根据打分函数确定一个具有最优结构的树，并将其加入模型当中。但这个过程的可能性几乎是无穷多种，我们可以以贪心的方式来构建，比如，从根节点开始，遍历所有的特征，针对每一个特征，先对该特征按照取值排序，然后进行线性扫描，获得最好的分割点，计算由这个特征加入所带来的增益（Gain），然后选取增益最大的特征作为当前节点的最终分裂特征。增益的计算方式为：

\[\text { Gain }=\frac{1}{2}\left[\frac{G_{L}^{2}}{H_{L}+\lambda}+\frac{G_{R}^{2}}{H_{R}+\lambda}-\frac{\left(G_{L}+G_{R}\right)^{2}}{H_{L}+H_{R}+\lambda}\right]-\gamma\]

表示分类后左子树的分数加上右子树的分数减去不分割时的分数，再减去加入新的叶子结点所带来的cost。

上述描述中有两点需要注意：

  1. 对于一个特征，按照其取值进行排序，线性扫描计算增益

    这里举一个例子，假设对年龄这个特征，我们可以按照年龄的大小对样本进行排序。假设有五个人$A,B,C,D,E$，则划分方式有以下四种（使用“$\mid$”符号表示划分）：

    • $A\mid B,C,D,E$
    • $A,B\mid C,D,E$
    • $A,B,C\mid D,E$
    • $A,B,C,D\mid E$

    每一种划分均将样本分成两个子集，针对每个子集，按照增益的计算方式，计算出分割点左右两侧样本集合的$g$和$h$，带入计算得到Gain即可。

    复杂度分析：$O(dKn\log n)$，其中，$d$为特征数，$n$为样本个数，$K$为树的层数。

    这里需要注意的一点是，由于需要对每个样本的当前特征计算$g$和$h$，样本之间的计算互不影响，因此这里可以引入并行计算来增加效率。

  2. 引入分割不一定使情况变得更好

    在一些情况下，可能出现分割后的增益太小的情况，这种分割会增大模型的复杂度，得不偿失，针对这种情况，XGBoost增加了有关叶子结点的惩罚项$\gamma$，即当分割所带来的收益小于$\gamma$时，取消此次分割，这里相当于对树做了预剪枝。

2）近似算法

对于连续性特征，样本数量过大，特征取值过多时，对特征的所有取值进行遍历选取最佳分割点的方式，会耗费较多的时间，针对此问题，XGBoost对特征进行分桶，即找到$l$个分位点，将相邻分位点之间的样本划分到同一个桶中，对该特征进行遍历时，仅需遍历这$l$个分位点即可。上述方式可以有两种应用方式：

  1. 在生成一棵树之前对各个特征进行分位点计算和样本划分，并在建树的过程中采用这种划分
  2. 在某一次具体的节点分裂时，采用这种分位点划分方式。

4.2.2 停止分裂条件

停止分裂条件定义了迭代算法的终止条件，一般地，XGBoost设置的停止分裂条件有如下几种：

  1. 当引入的分裂带来的增益小于给定阈值的时候，取消此次分裂，这里相当于预剪枝
  2. 设置一个树的最大深度参数max_depth，当分裂进行到此深度时则停止分裂，防止过拟合
  3. 当样本权重小于给定阈值时，停止建树，设置一个参数min_child_weight，当一个叶子结点包含的样本数量过少时，停止分裂
  4. 树的最大数量

4.3 算法细节

4.3.1 类别型特征处理

一些树学习方法分开考虑数值型特征和类别型特征，但XGBoost认为这种处理是不必要的，我们可以使用onehot编码将类别型特征转换为数值型特征，虽然当类别过多时会造成稀疏的现象，但对树学习算法的影响并不大。

4.3.2 剪枝和正则化手段

  1. 上文4.2.1 2）的分析中提到，在节点分裂阶段引入了分裂收益（Gain）这样一个指标，它的值可能是负的，在这种情况下，此次分裂不会被执行，这里相当于引入了预剪枝
  2. 提前终止，当某次分裂产生负收益时，提前终止分裂，但也有可能存在当前收益为负，但继续分裂后产生正收益的可能
  3. 后剪枝：先将树生长到最大深度，然后递归地从底向上对收益为负的叶子结点进行剪枝。

4.3.3 缺失值处理

在 分裂点计算过程中忽略缺失值样本，但为了保证完备性，会同时考虑将包含缺失值的样本分配到左子树和右子树两种情况，并选择Gain大的方向。

4.3.4 Shrinkage和列采样

这两个技术手段都是为了防止过拟合，本文4.1.1中介绍的Shrinkage，相当于对新的树的权重乘以一个缩放因子，类似于梯度下降法中的学习率，可以减小单颗树的影响程度。

与随机森林类似，XGBoost也使用了特征的列采样技术，具体地，仅通过特征集合的一个子集决定分裂点。

4.3.5 特征重要性

XGBoost通过三个指标判断特征的重要性：

  1. weight：在所有的树上，一个特征作为分裂特征的次数
  2. gain：该特征在所有树上带来的平均收益（average gain）
  3. cover：该特征在构建树的过程中影响到的样本数量

4.4 工程细节

4.4.1 Column Block

建树过程中最耗时的部分是最优切分点的寻找，更具体地，样本按特征取值进行排序。为了降低排序时间，提出Block结构来存储样本数据。

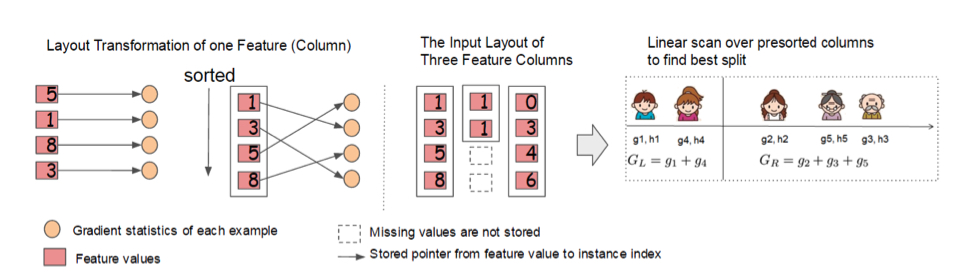
block

图3 Column Structure

4.4.2 Cache-aware Access

使用Block结构的一个缺点是，取梯度是通过索引来完成的，而由于梯度的获取顺序是按照特征的取值进行排序的，因此会导致非连续的内存访问，使得CPU cache命中率降低，影响算法的效率。

针对上述问题，XGBoost在每个线程中开辟一块缓冲区，将梯度信息预加载到其中，然后再进行统计；针对近似算法，动态地将块的大小设置为块内的样本个数。调整块的大小（block size）有助于在缓存性能和并行化之间找到一个均衡点。

4.4.3 Blocks for Out-of-core Computation

由于XGBoost在设计之初就考虑了对计算资源的高效利用，因此除了CPU、内存相关的优化外，对磁盘使用也进行了一定的优化：

对于大规模的训练数据，可以将数据分块保存在磁盘上，在计算过程中，使用独立线程将Block提取到主存缓冲区，达到计算和IO同步进行，同时，考虑到IO的耗时性，另外采用了两种技术来缓解：

  • Block Compression：块压缩，在加载到主存时由独立的线程负责解压缩
  • Block Sharding：块分片，将数据分配多个磁盘，每个磁盘的读取任务交由一个线程来处理，这样多个磁盘可以交替进行数据读取，增加整体的数据吞吐量。

4.5 总结

在介绍完XGBoost的原理和实现方案后，最后简单回顾一下，相比传统的GBDT，XGBoost都有哪些优点：

从目标函数的定义角度，XGBoost引入了代价函数的二阶导，对代价函数进行更好的拟合，基于泰勒近似的思想，使得使用者可以自定义任何二阶可导的损失函数，扩展了模型应用的灵活性；

从防止过拟合的角度，XGBoost引入了正则化项、Shrinkage、Column Subsampling，以及加入了基于交叉验证的早停策略；

其次，从运行速度来看，XGBoost针对CPU缓存命中、内存连续读取、IO并行访问等角度做了优化，同时，引入了Block结构，使得特征分裂点的计算过程实现了多线程并行运行。

参考

  1. 统计学习方法
  2. XGBoost: A Scalable Tree Boosting System
  3. July的XGBoost介绍
  4. Introduction to Boosted Trees By Tianqi Chen
  5. 树模型：XGBoost