在机器学习中,模型的训练过程即是在寻找一个足够好的函数$F^{\star}$,使得$F^{\star}$在训练数据和未来的新数据上都具有良好的推理效果。为了从候选函数空间$\{F\}$选择“好”的模型,人们引入损失函数的概念。一般地,对于样本$(x, y)$和模型$F$,假设模型对样本的预测值为$\hat{y}$,则损失函数被定义在$\mathbb{R}$的函数$l(y, \hat{y})$,用于描述预测值和真值的差距。
一般地,损失函数是一个有下确界的函数,这样,机器学习的优化过程即转化为了在数据集上的损失函数最小化问题。到目前为止,损失函数仅考虑了在训练数据上的经验风险,仅考虑经验风险,很有可能导致参数空间过于复杂,造成模型对训练数据过拟合。
模型复杂度¶
过拟合现象、泛化能力和模型复杂度三者之间联系紧密,模型复杂度取决于:
- 模型本身的选择
- 模型参数个数
- 模型的参数空间选择(当模型和参数个数都确定时,仍可以使用一些手段(如正则化),从参数空间中选择较优的参数)
当模型的复杂程度相对训练数据量过高时,就会发生过拟合现象,减轻过拟合现象的措施有:
- 使用更简单的模型
- 减少参数
- 在搜索参数空间时加入限制(如对参数增加正则化)
- 获取更多的样本
本文仅讨论使用正则化手段减轻过拟合的影响。
引入正则化¶
为了减轻模型的过拟合趋势,我们需要对损失函数中加入描述模型复杂程度的正则项$\Omega(F)$,优化过程转化为:
$$F^\star:=\mathop{\arg\min}_\limits{\theta} Obj(F)=\mathop{\arg\min}_\limits{\theta}(L(F)+\gamma\Omega(F)),\gamma>0$$
目标函数$Obj(\cdot)$描述模型的结构风险,其中$L(F)$表示模型在训练数据上的损失,$\Omega(F)$为正则化项,$\gamma$用于控制正则化项的强度,一般使用$L_p$范数作为正则项,用于对参数光滑度和参数空间范数上界进行限制,提升模型的泛化能力。
常见的用于正则化的$L_p$范数有以下几种:
- $L_0: \Vert W \Vert_0=\sum\limits^{d}_{i=1}I(w_i\neq 0)$
- $L_1: \Vert W \Vert_1=\sum\limits^{d}_{i=1}\vert w_i \vert$
- $L_2: \Vert W \Vert_2=\sum\limits^{d}_{i=1} w_i^2$
其中,$I(condition)$为指示函数,当$condition$成立时取$1$,否则取$0$。常用$L_1$和$L_2$正则化来限制模型的复杂度。
$L_1$和$L_2$正则化¶
从概率角度考虑,对模型参数施加的正则化项其实就是引入了参数的先验,$L_1$正则化对应Laplace先验,$L_2$正则对应高斯先验。这两种正则化都可以使参数变“小”。不同之处在于,$L_1$正则化可以使得参数稀疏化,可以用于特征选择;$L_2$正则化可以使得参数尺度受到约束,减轻过拟合现象。我们可以根据场景选择合适的正则化项,甚至可以同时使用二者,如stanford提出的ElasticNet就同时在模型中使用了$L_1$和$L_2$正则化,参考这篇1.2w次引用的slide。
$L_2$正则化能够通过减小参数尺度来减弱模型过拟合现象的原因¶
如果参数尺度很大,则对输入施加一个微小的扰动就会引起目标函数发生较大幅度的变化,也即模型对输入噪声的鲁棒性变差,过拟合风险增加。
$L_1$能够使模型参数变得稀疏的原因¶
下面以线性回归为例,简单分析$L_1$正则化会产生稀疏解的原因。
在线性回归中,如果加入$L_2$正则,则一般称为岭回归(Ridge regression);如果加入$L_1$正则,则一般称为Lasso回归。因此,$L_1$正则有时候也被称为Lasso正则。
Lasso回归的目标函数为:
$$L=\Vert XW-Y \Vert_F^2 + \lambda\Vert W \Vert_1$$
由于$ \Vert W \Vert_1=\sum\limits^{d}_{i=1}\vert w_i \vert$是一个包含局部不可导点的函数,因此,在优化过程中,不能使用常规的优化算法(如梯度下降法)。
有很多特殊的优化算法可以解决这一类优化问题,如LARS、Parallel CD、ADMM、Coordinate Descent等。Coordinate descent属于Sub-gradient descent范畴,以下介绍使用其进行参数求解。Coordinate descent的运行流程可以简化为:
循环执行以下直至收敛:
选择一个参数维度$i$
固定其余维度的参数
在第$i$维度上执行参数更新:$w_i\leftarrow w_i-\frac{\partial L}{\partial w_i}(W)$
$$Obj:L=\sum_\limits{i=1}^{n}\left(\sum_\limits{j=1}^{d} w_{j} x_{ij}+b-y_{i}\right)^{2}+\sum_\limits{j=1}^{d}\vert w_{j} \vert$$
$$\begin{aligned} \frac{\partial L}{\partial w_{l}} &=2 \sum_{i=1}^{n}\left(\sum_{j=1}^{d} w_{j} x_{i j}+b-y_{i}\right) \cdot x_{i l}+\frac{\partial\left|w_{l}\right|}{\partial w_{l}} \\ &=2 \sum_{i=1}^{n}\left(\sum_{j=1 \atop j\neq l}^{d} w_{j} x_{i j}+b-y_{i}+w_{l} x_{i l}\right) \cdot x_{i l}+\frac{\partial \vert w_{l}\vert}{\partial w_{l}} \\ &=2 \sum_{i=1}^{n}\left(\sum_{j=1 \atop j \neq l}^{d} w_{j} x_{i j}+b-y_{i}\right) \cdot x_{i l}+2 \sum_{i=1}^{n} w_{l} x_{il}^{2}+\frac{\partial \vert w_{l} \vert }{\partial w_{l}} \\ &=2 \sum_{i=1}^{n}\left(\sum_{j=1 \atop j \neq l}^{d} w_{j} x_{i j}+b-y_{i}\right) \cdot x_{i l}+2 w_{l} \sum_{i=1}^{n} x_{i l}^{2}+\frac{\partial \vert w_{l} \vert}{\partial w_{l}}\end{aligned}$$
设常数$2 \sum_\limits{i=1}^{n}\left(\sum_\limits{j=1 \atop j \neq l}^{d} w_{j} x_{i j}+b-y_{i}\right) \cdot x_{i l}$为$C_L$;设$2\sum_\limits{i=1}^{n} x_{i l}^{2}$为$a_L$,($a_L \gt 0$)。
则$\frac{\partial L}{\partial w_{l}}=C_{L}+w_{L} a_{l}+\lambda \cdot \frac{\partial \vert W_{l} \vert}{\partial l}$,分情况讨论:
$$\frac{\partial L}{\partial w_{l}}=\left\{\begin{array} \\C_{L}+a_Lw_l+\lambda&,w_l>0 \\ [C_L-\lambda,C_L+\lambda]&,w_l=0 &\\ C_L+a_Lw_l-\lambda&,w_l>0 \end{array} \right. $$
令$\frac{\partial L}{\partial w_{l}}=0$,可得:
$$\hat{w_l}=\left\{ \begin{array}\\ -C_L-\lambda &,if\ C_L\lt -\lambda\\ 0 &,if\ -\lambda \le C_L \le \lambda \\ \lambda-C_L &,if\ C_L\gt \lambda\end{array}\right.$$
由此可见,在更新第$l$维的权重时,当$-\lambda \le C_L \le \lambda$时,权重会被强制置为0,处于此范围的$C_L$导致了参数的稀疏化。
正则化做了什么¶
在参数优化过程中加入正则化,实际上是在一个确定的参数空间中,对参数的可行空间(feasible region)作了进一步约束,因此,假设$L$为模型在训练样本上的损失函数,我们可以得到如下结论:
$$L(\hat{w}_{without\ reg}) \leq L(\hat{w}_{with\ reg})$$
即,加入正则化后的参数在训练数据上的损失,一定不小于无正则化时的。
正则化的灵活运用¶
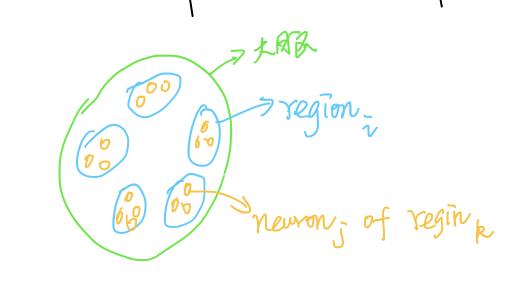
以简化的大脑神经元模型为例,假设大脑分为若干个区域(region),每个区域均包含一些神经元,每个神经元均具有对应的参数,$w_{ir_j}$表示大脑第$i$个神经元区域的第$j$个神经元的权重。
设目标函数为$f(W)$,我们期望通过正则化手段,将以下两个假设考虑进来:
- 某一个区域内,仅有少量神经元被激活
- 在空间上相近的神经元,作用类似
则我们可以构造如下优化目标:
$$\mathop{minimize}: f(W)+\sum\limits_{i=1}^R \lambda_i\Vert w _{i \cdot}\Vert_1+\sum\limits_{i=1}^{R}\sum\limits_{j=1}^{r_i}\lambda_2\Vert w_{ij}-w_{ij-1}\Vert_2$$
在上式中,$R$表示神经元区域个数,$r_k$表示第$k$个区域中包含的神经元个数,我们引入了两个正则化项,第一个用于神经元区域内的稀疏化,第二个用于约束相近神经元区域的相似程度。