Shihanmax's blog
动态时间规整（DTW）算法
工作中遇到了涉及不等长序列的近似度计算的问题，这里把阅读过的资料整理一下，方便以后参考。
1. 概述
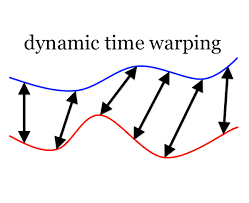
在序列相似度比较的任务中，对于一些在某个维度上可以延展或者压缩的信号来说，如果直接使用传统的序列距离计算方法（如欧式距离）来衡量序列的相似度的话，是不合适的。（如同一个人慢速和快速讲同一句话。）
这个时候，我们需要对待比较的若干组序列信息从某个维度上进行延展或压缩，使得序列之间更好地对其（如波峰、波谷的对齐），对语音信号来说，也就是对语音波形在时间轴上进行规整，DTW算法称这种操作为Wrapping。
2. DTW
这里以两个待比较的时间序列$P$、$Q$为例：$P$的长度为$m$、$Q$的长度为$n$，则序列$P$、$Q$分别为：
\[P=p_1,p_2,...p_i,...p_m\] \[Q=q_1,q_2,...,q_j,...q_n\]目标：合理地计算出序列$P$、$Q$的相似度
无论$m$和$n$是否相等，我们都需要对序列中的元素进行对齐，（比如线性缩放，但线性缩放明显不满足我们的要求。）
为了对其$P$和$Q$，需要构造一个$m \times n$的矩阵$A$，其中$A(i,j)$代表$P_i$和$Q_j$两个元素的距离$d(P_i,Q_j)$，这个距离计算函数$d(\cdot)$可以是适合的相似度计算方法，如简单的欧氏距离。对齐点的寻找相当于在矩阵A中寻找一个经过若干个格点的一条路径，该路径上任一点$P(x,y)$表示序列中$P_x$与$Q_y$对齐。
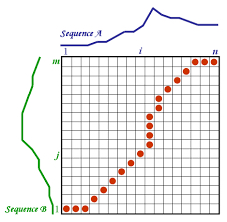
我们将；路径定义为Wrapping Path，用$W$表示，$W$的第$k$个元素为：
\[W_k=(i,j)_k\] \[W=w_1,w_2,...,w_K\quad \quad max(m,n)\le K\lt m+n-1\]路径W应满足一下约束：
- 边界条件：$W_1=(1,1)$，$W_K=(m,n)$，即两序列的起始和终止位置必须对齐
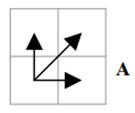
- 连续性：如果$W_{k-1}=(a’,b’)$，则$W_k=(a,b)$必须满足$(a-a’) \le 1$且$(b-b’) \le 1$
- 单调性：如果$W_{k-1}=(a’,b’)$，则$W_k=(a,b)$必须满足$(a-a’) \ge 0$ 且$(b-b’) \ge 0$，此条保证路径随时间单调进行
通过2、3两个条件的约束，在路径$W$的任意位置，寻找下一个路径点时，路径的行进方向仅有三种可能：
满足上述约束条件的路径数量有指数多种，我们要寻找的是，使得规整代价最小的路径:
\[DTW(P,Q)=min(\sqrt{\sum_{k=1}^K} /K)\]DTW的思想是将两个序列在时间维度上进行延伸和压缩，最终得到一个最短的路径，这个距离也即是两个序列的距离度量。
最短路径可以使用动态规划计算，定义累加距离$\gamma$，在矩阵$A$的某一格$A(i,j)$上，累加距离的递推公式为：
\[\gamma_{i,j}=d(p_i,q_j)+min(\gamma_{i-1,j-1},\gamma_{i-1,j},\gamma_{i, j-1})\]